-> GJK Algorithm <-

Casey Muratori’s tutorial and Igor Kroitor’s Github Page are must-see-reference.

GJK algorithm is an algorithm for collision detection for convex polygon. Only 2D is implemented/tested/coded here.

The basic idea:

1. Get Minkowski difference between two polygons.
2. If the result shape contains origin (0,0,0), there are intersection between the polyons. No intersection if origin is not within the result shape.

The ‘detail’ process (to have a better understanding, please refer to the reference link above):

1. Support function
   1. Get the furthest point using Minkowski difference from two polygons with the direction vector provided and put it in a container (for simplexes).
2. Loop
   1. First, get another simplex point using Support function with opposite direction vector.
      Note: if the dot product of new point and the search direction vector is lesser than 0, means the new point does not pass through origin, so it is impossible for the result shape to contain origin. Thus, not collision.
   2. Second, get third point using Support function with direction vector pointing toward origin from the line formed by the previous 2 points in simplex container. 3D will be a tetrahedron/3-simplex (0-simplex is a point, 1-simplex is a line, 2-simplex is a triangle etc.)
   3. For 2D, if there are 3 points to form a triangle, check if the triangle contains origin.
   4. If origin is found, there is collision.
   5. If not, there isn’t. Continue to Support function by providing a direction vector toward origin then Loop again.

My Implementation

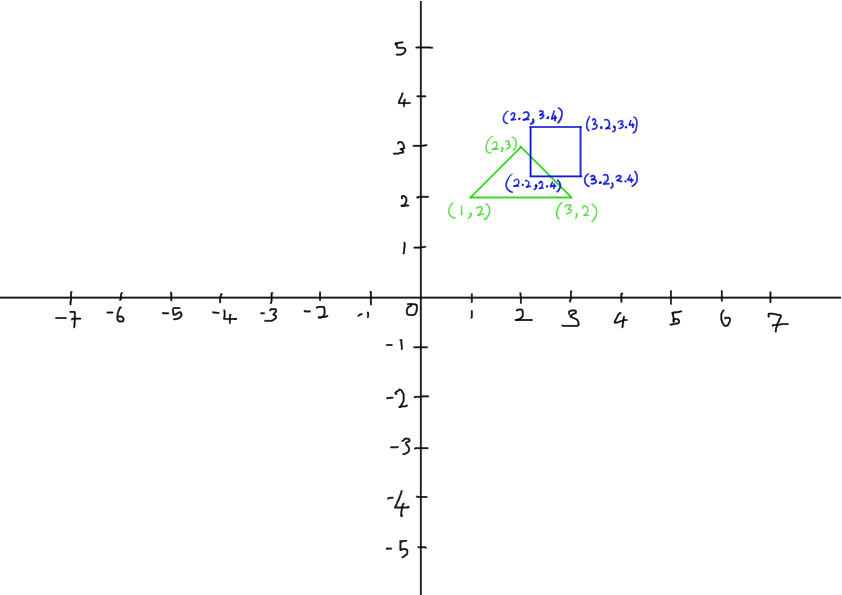
1. There are two convex polygon, triangle and squares.

Based on the GJK theory, I should calculate the algorithm using as much vertex points as possible.

However, for the sake of simplicity, I just use at most 4 vertex points to run the GJK algorithm.

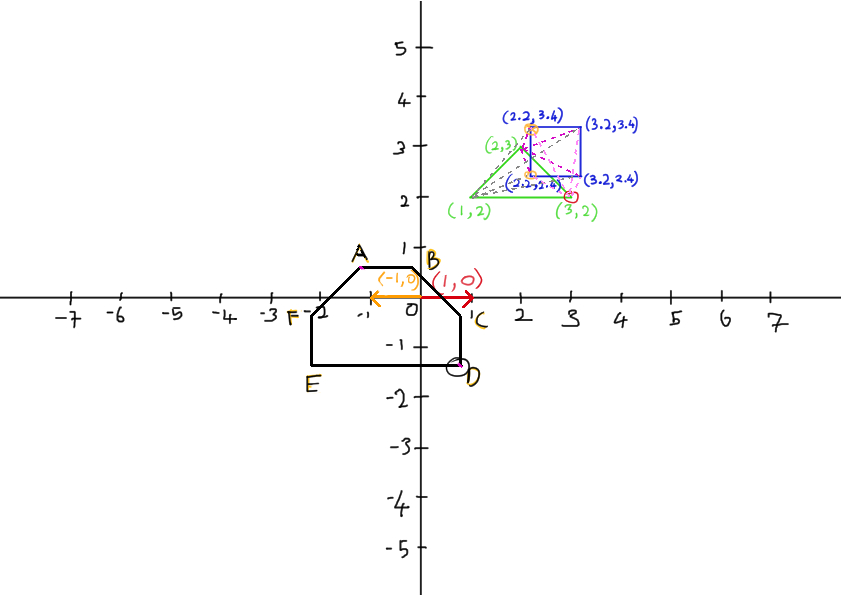
1. To get Minkowski Space, I calculate the difference (or sum of Shape A + (- Shape B)) by using three vertices of triangle against each vertices of the square.

The black color polygon is the result shape in Minkowski Space.

Using out naked eyes, it is pretty easy to tell if the origin point is inside the result shape. However, the machine cannot tell without running some code.

So I pick a direction, in this case, to the right (1 , 0) and input the direction (red arrow) to support function and get the relative point in triangle (red circle).

To make sure the result point is at the edge of the result shape in Minkowski Space, the opposite direction (orange arrow) is inputted for getting a point from square (orange circle).

By doing the calculation, point from triangle - point from square, point D in Minkowski Space is found and put in the simplex container.

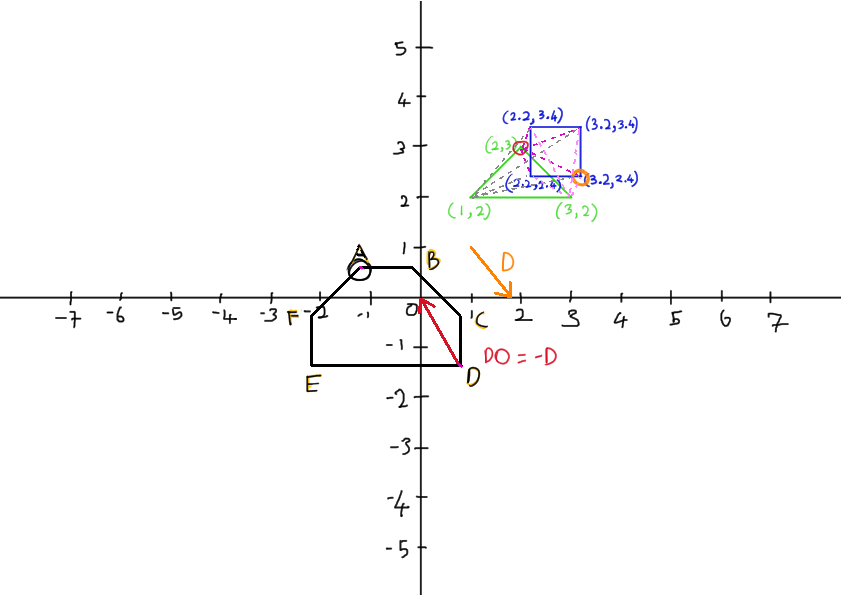
1. Theoretically, we can find any other points to form the simplex. But to make things easier, I set the new direction as DO for the support function.

As my ultimate goal is to determine if the result shape contains origin, I pick the direction to point towards origin.

Then continue to get the difference of two new points from triangle and square as method mentioned in step 2.

If the dot product of result point and the direction (DO) is lesser than 0, means the result point never pass through origin, which means the result shape in Minkowski Space does not contain origin. In other words, there is no collision.

In the image above, the result point is A, which is above origin (dot product of A and the direction (DO) will be > 0, since they are facing in the same direction).

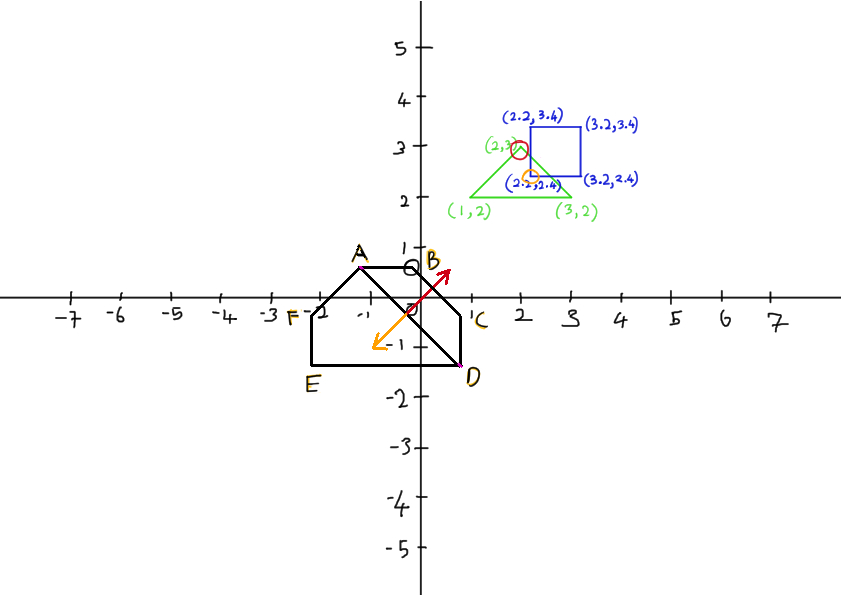
1. Now, I have a line AD after I put A into the simplex container.

Again, repeat the above steps (2 and 3), but using the perpendicular of line AD as it perpendicular line will be facing origin.

Using cross product of AD and DO/AO, I get the perpendicular line going out/in (based on DO/AO and the result can be known using right hand rule) the image.

The perpendicular line is then used to calculate the direction towards origin from the AD line by cross product it with DO/AO (again, depends on what we used just now). The equation, for example, will be: AD X DO X AD. **Triple product can be used to calculate the resulting perpendicular line too.

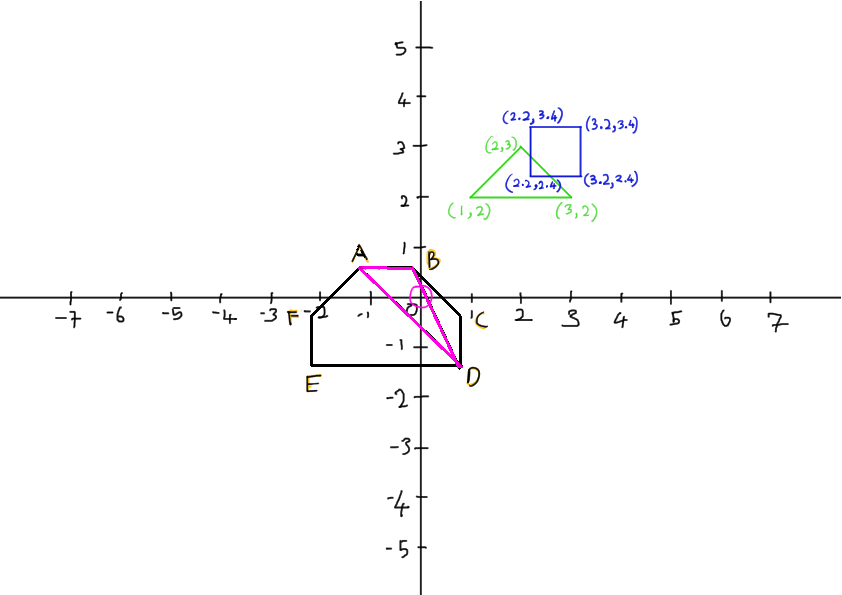
1. After putting the new found point in the simplex container, now is left with checking if the triangle form by simplex contains origin.

To check if the origin is contained, in this case, there are A, B, D points for the triangle. A, B, and D are really just the simplex I found before.

As before, I calculate the dot product of the perpendicular line of AB and point D. If it is lesser than 0, means origin is beyond point D. In other words, it does not contain origin.

If it is not lesser, I repeat the calculation with BD and A, and lastly, DA and B. Basically three lines of triangle against the opposite point.

If all results return true, there is collision.

In this case, there is collision as showed in the image.

If not, go back to step 2 and loop again with different direction and hence, different point.

For the sake of simplicity, I just remove the point that is furthest away from origin in the simplex container.

This way, the result may not be 100% accurate, but it is certainly sufficient enough for collision checking in my multiplayer shooter game.